ADQUISICION Y
PROCESAMIENTO DE SEÑALES
CONCEPTOS Y
APLICACIONES
Un convertidor analógico-digital es un
dispositivo que transforma una señal (usualmente voltaje) en una cadena de
bits. Estas cadenas se almacenan en un archivo de computadora o se procesan en
tiempo real. Para realizar una medida, de manera que se reproduzca
fehacientemente un cierto fenómeno, hay que seguir ciertos pasos, que se
señalan a continuación:
-
Determinación de los valores mínimo y máximo de la señal.
-
Estimación de la frecuencia o frecuencias que aparecen en la señal.
-
Elección de la frecuencia de muestreo
-
Acondicionamiento y filtrado de la señal.
-
Elección de la resolución del sistema de adquisición de datos
-
Selección del tamaño de la muestra
Los sistema de conversión a/d operan por lo
general en el intervalo [-10V, +10V], por lo que la señal debe de estar
comprendida dentro de estos límites. Si el transductor produce valores de
milivolts, entonces es necesario amplificarla para que al ingresar al sistema
de conversión analógico-digital se tengan valores del orden de volts. En
ocasiones es posible reducir el intervalo de conversión del dispositivo, por
ejemplo de [-5V,5V] o bien
[-1V,1V].
Por el contrario, si la señal excede en magnitud el valor de 10V, se
hará necesario reducir su amplitud. Esto por ejemplo se puede lograr si se
utiliza una punta de osciloscopio que reduce en un factor 10 el valor de
voltaje.
Es muy común tener captores que tienen
salidas en milivolts, algunos de ellos son los dispositivos piezoeléctricos
para la medición de presión y fuerza o las sondas de platino para medir la
temperatura en aire. Otro caso es el de
los micrófonos sin amplificador cuya función es convertir fluctuaciones de
presión en el aire en impulsos eléctricos. Todas estas señales se pueden ver en
un osciloscopio.
En otras circunstancias los voltajes son de
unas cuantas unidades. Por ejemplo, esto ocurre en un circuito R-C cuando se
alimenta a este con una bateria de 1.5 o 9 volts. Por lo tanto, aquí no se
requiere aplicar amplificación. El valor mínimo en cualquiera de los
componentes del circuito (es decir, en la resistencia o el capacitor) es cero y
el valor máximo es el voltaje de la batería.
Es muy importante que la señal que se envia
al convertidor A/D no exceda los valores límites por dos razones: a) una señal
de amplitud mayor al máximo permitido puede dañar al dispositivo y b) cuando se
exceden los valores límites el convertidor ya no reproduce el comportamiento de
la señal, sino que queda registrado como único valor el máximo. Esto queda bien
establecido en las figuras 1 y 2.

Figura
1 .- señal senoidal de amplitud 12.5. Se ha graficado solo medio periodo.
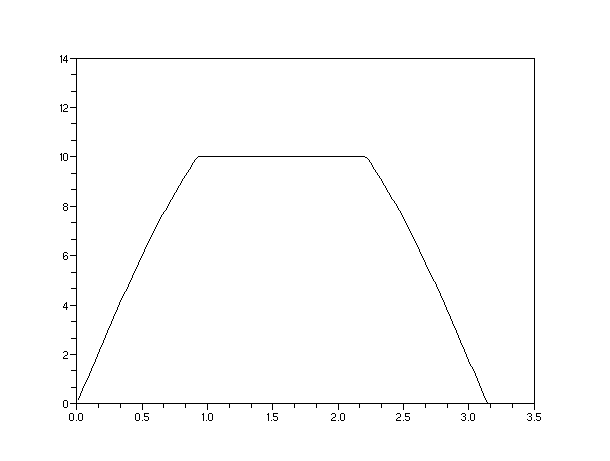
Figura
2.- Secuencia de datos que se registran con el convertido a/d. Cuando se excede
el valor 10, ocurre un error de desbordamiento y todos los valores quedan
guardados como un valor de voltaje igual a
10.
ESTIMACION DE
FRECUENCIAS PRESENTES EN LA SEÑAL
Considerese una función f(t) de periodo T, es
decir f(t)=f(t+T) para cualquier valor
de t. La función se puede desarrollar como una combinación lineal de funciones
trigonométricas:
![]()
Los
coeficientes se calculan de la siguiente manera:
![]()
![]()
![]()
La cantidad ![]() representa la intensidad de la componente de frecuencia
representa la intensidad de la componente de frecuencia ![]() en la función
f(t). Al realizar una grafica de cn
vs n se puede determinar para qué índice se alcanza el valor mayor de cn
y este nos permitirá conocer cuál es la o las frecuencias dominantes en la
función.
en la función
f(t). Al realizar una grafica de cn
vs n se puede determinar para qué índice se alcanza el valor mayor de cn
y este nos permitirá conocer cuál es la o las frecuencias dominantes en la
función.
Una
herramienta muy útil en el estudio de fenómenos físicos es la transformada de
Fourier. Desde un punto de vista matemático se le define como:

Se trata de una operación sobre una función
que permite conocer las amplitudes de las diferentes componentes en frecuencia.
La transformada de Fourier es una generalización de las series de Fourier, para
funciones de periodo arbitrario.
Cuando se dispone de un conjunto finito de
datos no se tiene la posibilidad de evaluar la integral anterior y entonces se
recurre al algoritmo de la transformada discreta de Fourier. Y cuando el número
de datos es una potencia de 2, se usa un algoritmo que reduce el tiempo de
calculo y que lleva el nombre de transformada de rápida de Fourier (en inglés
lleva el nombre Fast Fourier Transform o FFT). En cualquier caso la,
transformada de Fourier discreta permite calcular las intensidades de 0 hasta
la mitad de la frecuencia de muestreo.
Las señales monocromáticas son mas bien una excepción,
estas se pueden producir con un generador de funciones o son el resultado de
experimentos como el oscilador armónico. Su transformada de Fourier es cero
para casi todos los valores, excepto para la frecuencia de la propia señal. Supóngase
que se muestrea la señal f(t)=2.5sen(2p100t) a razón de 5000
datos/segundo durante un intervalo de tiempo de 2 segundos. Al calcular la
transformada de Fourier con 213=8192 datos se obtiene el resultado
mostrado en la figura 3:
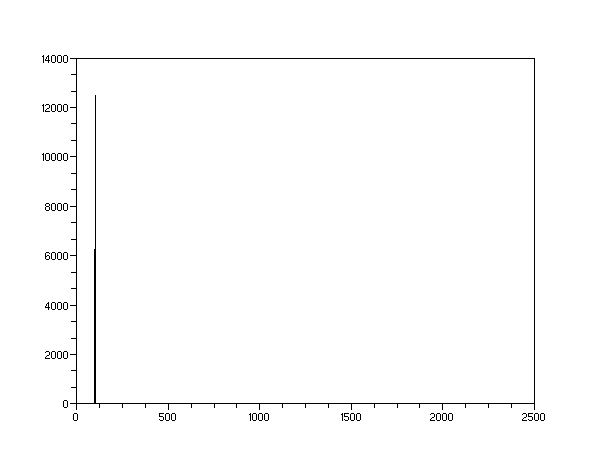
Figura 3.- Transformada de Fourier de una señal monocromática. Existe
un pico muy marcado que corresponde a la frecuencia de la señal, que es de 100
Hz.
En otras circunstancias la transformada de
Fourier tiene un aspecto diferente. Por ejemplo para una señal de velocidad de
un flujo turbulento, las intensidades de las frecuencias siguen una ley de
potencias en un intervalo, por lo que se debe de hacer la grafica en escala
log-log, tal como se muestra enseguida:

Figura 4.- Grafica de la
transformada de Fourier de una señal de velocidad en un flujo turbulento. La
velocidad de muestreo es de 20,000 datos/segundo. Se ha usado escala
logarítmica en ambos ejes para mostrar que hay un intervalo de frecuencias
donde hay un comportamiento de ley de potencias.
Para el calculo de la anterior figura se han
tomado 750 segmentos de 8192 datos, en cada uno de ellos se ha evaluado la
transforma rápida de Fourier y luego se ha promedio. Con ello se ha eliminado
el “ruido” que contiene una sola
evaluación de la FFT.
La transformada de Fourier permite determinar
las frecuencias relevantes en una señal. El procedimiento que se debe seguir es
probar con varias tasas de muestreo, calcular la FFT y determinar cuáles son
las frecuencias importantes.
Cuando ya se han determinado las frecuencias
relevantes, surge otra cuestión: ¿que frecuencia de muestreo elegir?. Para ello
es necesario usar un teorema que será descrito en la siguiente sección.
TEOREMA DE NYQUIST
El teorema de Nyquist establece lo siguiente:
Para la reconstrucción de una
señal se debe elegir una frecuencia de muestreo por lo menos del doble de la
frecuencia relevante más alta de la cantidad que se está midiendo.
Vamos a dar algunos ejemplos de los errores
que se cometen cuando no se sigue este criterio. Consideremos una señal monocromática
con frecuencia n=500 Hz. ¿Qué ocurre si
muestreamos justamente a la frecuencia de 500 Hz?. Esto se puede observar en la
figura 5:

Figura 5.- Resultado
obtenido cuando la frecuencia de muestreo y la frecuencia de una señal
monocromática coinciden. Todos los datos
son iguales entre si, lo que dista mucho de representar a la señal original.
Enseguida supongamos que se muestrea a una
frecuencia un poco superior a 500 Hz, digamos a 505 Hz. El resultado se muestra en la figura 6:

Figura 6 .- Resultado de
hacer una adquisición la señal a una
frecuencia un poco superior a 500 Hz.. Lo que se observa es una grafica de una
señal con una frecuencia igual a la diferencia f-n. Esto no es una
representación fidedigna de la señal.
Ahora consideremos que la señal se muestrea a
una tasa de 5000 Hz. El resultado se presenta en la figura 7.
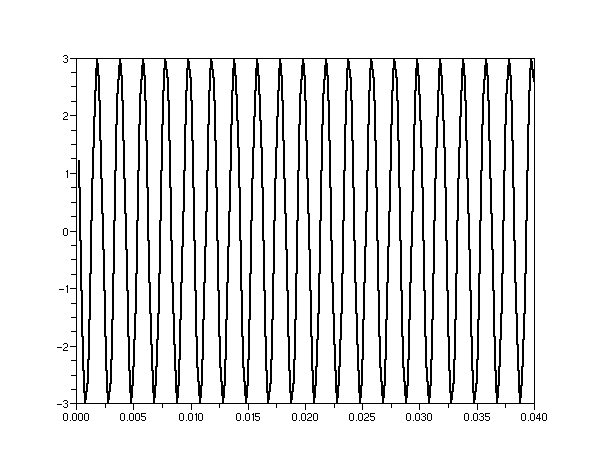
Figura 7 .- Resultado del
muestreo de la señal a razón de 5000 datos/segundo. En la grafica se muestra un
intervalo de tiempo de 0.040 segundos, en donde aparecen 20 periodos. Lo que significa
que en un segundo hay 500 periodos.
RESOLUCION DE LA
TARJETA DE ADQUISICION
Los dispositivos actuales de conversión
analógico/digital tienen resoluciones de 8, 12, 16, 23 o 24 bits. Pero ¿Qué
significa esto?
La señal es una función continua en el
tiempo. Sin embargo durante la digitalización,
se hace una discretización en dos sentidos:
- Se tiene una serie de tiempo con N datos
- Los valores de la señal se redondean
El número de datos N está relacionado con la frecuencia de muestreo f y
el tiempo total de adquisición (t) por medio de la relación: N=tf. Por otra parte,
el redondeo de la señal se relaciona con la resolución del dispositivo y con el
intervalo de operación de la tarjeta. Pongamos un ejemplo: supóngase que se ha
elegido como intervalo de operación [-2,
2] volts y que el sistema de adquisición de datos tiene una resolución de 16
bits. Esto último significa que el dispositivo toma 216=65536
valores diferentes dentro del intervalo de operación. Estos son:
(-2.00, -2.00+Dx,-2.00+2Dx, -2.00+3Dx, ….., -2.0+(216-1)Dx)
el valor del incremento Dx es igual a la
longitud del intervalo de operación dividido entre 2 elevado a la resolución
del aparato. Para nuestro caso ![]() volts o bien 0.06
milivolts. Cuando la señal ingresa a la tarjeta no se registra el valor exacto,
sino que se toma el valor más próximo del conjunto dado anteriormente. Es lo mismo que ocurre cuando
se mide con una regla graduada en milímetros. El valor que se reporta al medir
el lado de una hoja es el que se obtiene de poner un extremo de la regla en un
extremo y determinar cual es la marca más próxima en el extremo opuesto.
volts o bien 0.06
milivolts. Cuando la señal ingresa a la tarjeta no se registra el valor exacto,
sino que se toma el valor más próximo del conjunto dado anteriormente. Es lo mismo que ocurre cuando
se mide con una regla graduada en milímetros. El valor que se reporta al medir
el lado de una hoja es el que se obtiene de poner un extremo de la regla en un
extremo y determinar cual es la marca más próxima en el extremo opuesto.
Los sistemas actuales llegan a tener resoluciones hasta de 24 bits, lo
que vuelve innecesario una amplificación previa para muchas señales pequeñas.
Sin embargo, para los dispositivos de resolución menor la amplificación sigue
siendo necesaria. Considérese el siguiente caso: se usa un captor
piezoeléctrico de presión para determinar como se va llenando un recipiente (p=rgh, en donde h
es la profundidad, g el valor de la gravedad y r la densidad del fluido). Los valores de la
señal de salida del captor piezoeléctrico son 5 mV para cuando el recipiente
esta vacío (profundidad cero) y de 20 mV para cuando se ha llenado. Si se usa
una tarjeta de 12 bits de resolución y se trabaja en el intervalo [-10,10] volts,
entonces el valor de Dx es:
![]()
Por lo tanto los valores que quedarían registrados en el llenado del
recipiente serían: 4.88 mV, 9.76 mV,
14.64 mV y 19.52 mV. Aparentemente el llenado ocurre en cuatro
saltos, perdiéndose el comportamiento
intermedio. Si la señal se amplifica por
un factor 200, los valores que ingresan a la tarjeta están comprendidos entre 1 y 4 volts. Pero en el intervalo [1,4] la tarjeta convierte la señal a 614 valores
distintos y entonces se tiene más detalle del fenómeno.
A veces una señal tiene un valor
promedio grande en comparación con la intensidad de las fluctuaciones, pero lo
que nos interesa es investigar a las fluctuaciones. En estas circunstancias el
procedimiento que se sigue es restar a la señal un valor constante (llamado
offset) y registrar solo las
fluctuaciones. Esto no es lo mismo que el acoplamiento AC que se usa en varios
equipos electrónicos, puesto que siempre se tiene información del offset que se
ha aplicado a la señal. El paso siguiente es aplicar una amplificación sobre la
señal resultante. Un caso donde se
aplica este procedimiento es en la medición de velocidad en un flujo con una
sonda de hilo caliente. Vamos a
considerar que el voltaje está comprendido entre 1.53 y 1.69. Si la medición se
realiza sin aplicación de offset y ganancia, una tarjeta de adquisición de 12 bits va a
convertir la señal en 33 valores distintos. Si por el contrario se aplica un
offset de 1.60 volts y luego se hace una amplificación de 50, la señal
resultante estará comprendida entre -3.5 y 4.5 volts. Y entonces el sistema de
adquisición aumenta su resolución, pudiendo diferenciar entre 1638 valores
distintos.
FILTRADO
El filtrado es un elemento muy importante a considerar. Existen 3 tipos
de filtro:
a) filtro pasa-bajos. Es una operación que
teóricamente elimina de una señal las componentes con una frecuencia superior a
un valor umbral n. n es la
frecuencia de filtrado.
b) filtro pasa-altos. Es una operación que
teóricamente elimina de una señal las componentes de frecuencia inferior a un
valor umbral n.
c) Filtro
pasa-banda. Es una operación que elimina de la señal las componentes de
frecuencia inferiores a un valor n1 y las componentes de frecuencia superiores a n2. Dicho de otra manera, un filtro pasa-banda
es una composición de un filtro pasa-bajos y un filtro pasa-altos.
La señal se puede
filtrar con un dispositivo electrónico o también de forma digital, es decir, aplicando esta
operación luego de la toma de los datos. La operación que más se usa es la del
filtro pasa-bajos, puesto que las intensidades de las componentes de
frecuencias altas en una señal decrecen con el crecimiento de esta, mientras
que el ruido llega a ser el factor dominante, enmascarando completamente a la
señal. A veces los factores que producen ruido no se pueden eliminar
completamente, pero esto no es un problema si las frecuencias características
de la señal y del ruido son muy distintas.
Para entender mejor el significado de un filtrado podemos recuperar las ideas de la
transformada de Fourier. Una función se aproxima con una suma de funciones
trigonométricas. Un filtro pasa-bajos consiste en eliminar de la suma anterior
los primeros términos. Por otra parte, un filtro pasa-altos consiste en
eliminar de la suma los términos por arriba de cierto índice.
En ciertas ocasiones se requiere amplificar
las componentes de una señal alrededor de una cierta frecuencia. Esto se hace
con un dispositivo electrónico conocido como amplificador lock-in.
Con el objeto de satisfacer el teorema de
Nyquist y así evitar problemas de muestreo incorrecto, se debe de filtrar la
señal a una frecuencia inferior a la mitad de la frecuencia de adquisición.
ELECCION DEL
TAMAÑO DE LA MUESTRA
La
cantidad de datos que se deben registrar depende de varios factores. El primero
a considerar es la escala de tiempo (t) del fenómeno que se está
estudiando. El tamaño de la muestra debe de cubrir un intervalo de tiempo
mayor, es decir:
N > t f
En
donde f es la frecuencia de muestreo. Pongamos el caso de la descarga de un
circuito R-C cuya constante de tiempo
es RC=0.22 segundos. Si la frecuencia de muestreo es de 5000 datos/segundo, el
valor de N debe ser mayor a 5000x0.22=1100. Considerando que va a transcurrir
un intervalo entre el inicio de la toma de datos y el cierre del circuito RC,
un valor de N que se ha tomado en varios experimentos es de 2 segundos (ver
manual de operación de las tarjetas de adquisición de datos).
Otro
factor tiene que ver con el calculo de la frecuencia dominante de una señal.
Esto se puede ver cuando se estudia el efecto Doppler acústico. Supóngase que
se produce un sonido monocromático de 1000 Hz
y luego se quiere medir el corrimiento en frecuencia cuando el emisor se
mueve a una velocidad de 1 m/s. Teóricamente este corrimiento es de:
Dn=2.94 Hz
La
frecuencia dominante se obtiene calculando la transformada de Fourier. Esta se
obtiene usando un número de datos igual a una potencia de 2 (transforma rápida
o FFT). El algoritmo nos da valores para frecuencias entre 0 y la mitad de la
frecuencia de adquisición. La resolución de la transformada de Fourier es:
![]()
en
donde 2p es el tamaño de la muestra donde se calcula la transformada.
Para el ejemplo, supóngase que f=10,000 datos/segundo y queremos que ![]() n
sea menor a 0.5 Hz. Esto nos lleva a que
el tamaño de la muestra debe ser mayor a 10,000/0.5=20,000 datos. Como N tiene
que ser una potencia de 2, se toma la más próxima a este número, es decir
32768.
n
sea menor a 0.5 Hz. Esto nos lleva a que
el tamaño de la muestra debe ser mayor a 10,000/0.5=20,000 datos. Como N tiene
que ser una potencia de 2, se toma la más próxima a este número, es decir
32768.
En la figura 8 aparece la grafica de la transformada de Fourier para un experimento realizado en tales condiciones.

Figura 8.- Transformada de
Fourier para una fuente en reposo que emite a 1000 Hz y para la misma fuente,
pero moviéndose a 1 m/s. Se aprecia claramente el corrimiento de frecuencia del
pico.
En principio debe
tomarse la mayor cantidad de datos para
hacer un cálculo satisfactorio de cantidades estadísticas. Sin embargo,
se esta limitado por el tamaño de los dispositivos de almacenamiento. Un camino que se ha seguido desde el
surgimiento de los dispositivos de conversión analógico-digital es el
almacenamiento comprimido de los datos. En este sentido es preferible que durante
un experimento los datos se guarden en archivos binarios, en lugar de archivos
de texto. Un convertidor a/d de 12, 14 o 16 bits requiere solo de 2 bytes para
almacenar un dato, sin embargo si se decide escribir los valores en archivos de
texto, cada carácter ocupa un espacio de un byte y además los espacios, los
saltos de línea o de página requieren de espacio adicional.